Este rabisco de graffiti de 180 anos foi na verdade uma equação que mudou a história da matemática

Em 16 de outubro de 1843, o matemático irlandês William Rowan Hamilton teve uma epifania durante uma caminhada ao longo do Canal Real de Dublin. Ele ficou tão entusiasmado que pegou seu canivete e gravou sua descoberta ali mesmo, na ponte Broome.
É o graffiti mais famoso da história da matemática, mas parece bastante modesto:
eu ² = j ² = k ² = ijk = –1
No entanto, a revelação de Hamilton mudou a forma como os matemáticos representam a informação. E isso, por sua vez, simplificou inúmeras aplicações técnicas — desde o cálculo de forças ao projetar uma ponte, um ressonância magnética máquina ou turbina eólica, até programar mecanismos de busca e orientar um veículo espacial Marte. Então, o que significa esse famoso grafite?
Objetos giratórios
O problema matemático que Hamilton estava tentando resolver era como representar a relação entre diferentes direções no espaço tridimensional. A direção é importante na descrição de forças e velocidades, mas Hamilton também estava interessado em rotações 3D.
Os matemáticos já sabiam representar a posição de um objeto com coordenadas como x, sim e zmas descobrir o que aconteceu com essas coordenadas quando você girou o objeto exigiu uma geometria esférica complicada. Hamilton queria um método mais simples.
Ele foi inspirado por uma forma notável de representar rotações bidimensionais. O truque era usar o que é chamado de “números complexos“, que têm uma parte “real” e uma “imaginário“parte. A parte imaginária é um múltiplo do número eu“a raiz quadrada de menos um”, que é definida pela equação eu ² = –1.
Relacionado: Números imaginários podem ser necessários para descrever a realidade, segundo novos estudos
No início de 1800, vários matemáticos, incluindo Jean Argand e John Warren, descobriram que um número complexo pode ser representado por um ponto num plano. Warren também mostrou que era matematicamente bastante simples girar uma linha em 90° neste novo plano complexo, como girar o ponteiro de um relógio das 12h15 para o meio-dia. Pois é isso que acontece quando você multiplica um número por eu.
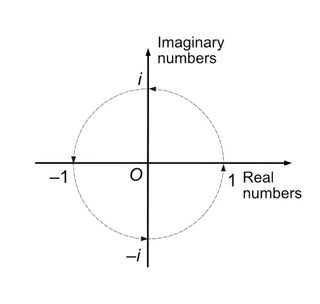
Hamilton ficou muito impressionado com esta ligação entre números complexos e geometria, e começou a tentar fazê-lo em três dimensões. Ele imaginou um plano complexo 3D, com um segundo eixo imaginário na direção de um segundo número imaginário jperpendicular aos outros dois eixos.
Ele levou muitos meses árduos para perceber que, se quisesse estender a magia rotacional 2D da multiplicação por eu ele precisava quatronúmeros complexos dimensionais, com um terceiro número imaginário, k.
Neste espaço matemático 4D, o k-axis seria perpendicular aos outros três. Não só faria k ser definido por k ² = –1, sua definição também é necessária k = eu = –ji. (Combinando essas duas equações para k dá QI = –1.)
Juntando tudo isso dá eu ² = j ² = k ² = QI = –1, a revelação que atingiu Hamilton como um raio na ponte Broome.
Quatérnios e vetores
Hamilton chamou seus números 4D de “quatérnios” e os usou para calcular rotações geométricas no espaço 3D. Este é o tipo de rotação usado hoje para mover um robô, digamos, ou orientar um satélite.
Mas a maior parte da magia prática surge quando você considera apenas a parte imaginária de um quaternion. Pois foi isso que Hamilton chamou de “vetor”.
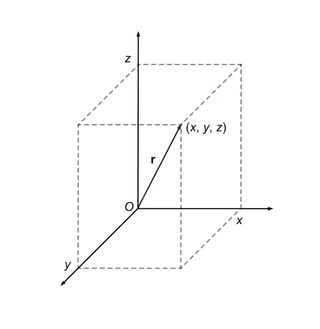
Um vetor codifica dois tipos de informação ao mesmo tempo, sendo o mais famoso a magnitude e a direção de uma quantidade espacial, como força, velocidade ou posição relativa. Por exemplo, para representar a posição de um objeto (x, sim, z) em relação à “origem” (o ponto zero dos eixos de posição), Hamilton visualizou uma seta apontando da origem para a localização do objeto. A seta representa o “vetor de posição” x eu + sim j + z k.
Os “componentes” deste vetor são os números x, sim e z — a distância que a seta se estende ao longo de cada um dos três eixos. (Outros vetores teriam componentes diferentes, dependendo de suas magnitudes e unidades.)
Meio século depois, o excêntrico telegrafista inglês Oliver Heaviside ajudou a inaugurar a análise vetorial moderna, substituindo a estrutura imaginária de Hamilton eu, j, k com vetores unitários reais, eu, j, k. Mas de qualquer forma, os componentes do vetor permanecem os mesmos — e, portanto, a seta e as regras básicas para multiplicar vetores também permanecem as mesmas.
Hamilton definiu duas maneiras de multiplicar vetores. Um produz um número (hoje chamado de escalar ou produto escalar) e o outro produz um vetor (conhecido como vetor ou produto vetorial). Essas multiplicações surgem hoje em uma infinidade de aplicações, como a fórmula da força eletromagnética que sustenta todos os nossos dispositivos eletrônicos.
Um único objeto matemático
Sem o conhecimento de Hamilton, o matemático francês Olinde Rodrigues tinha inventado uma versão destes produtos apenas três anos antes, no seu próprio trabalho sobre rotações. Mas chamar as multiplicações de Rodrigues de produtos de vetores é uma retrospectiva. Foi Hamilton quem ligou os componentes separados em uma única quantidade, o vetor.
Todos os outros, de Isaac Newton a Rodrigues, não tinham o conceito de um único objeto matemático unificando os componentes de uma posição ou de uma força. (Na verdade, houve uma pessoa que teve uma ideia semelhante: um matemático alemão autodidata chamado Hermann Grassmann, que inventou de forma independente um sistema vetorial menos transparente ao mesmo tempo que Hamilton.)
Hamilton também desenvolveu uma notação compacta para tornar suas equações concisas e elegantes. Ele usou uma letra grega para denotar um quaternion ou vetor, mas hoje, seguindo Heaviside, é comum usar uma letra latina em negrito.
Esta notação compacta mudou a forma como os matemáticos representam quantidades físicas no espaço 3D.
Tomemos, por exemplo, uma das equações de Maxwell relacionando os campos elétrico e magnético:
∇ × E = –∂B/∂t
Com apenas alguns símbolos (não entraremos no significado físico de ∂/∂t e ∇ ×), isso mostra como um vetor de campo elétrico (E) se espalha pelo espaço em resposta a mudanças em um campo magnético vetor (B).
Sem a notação vetorial, isso seria escrito como três equações separadas (uma para cada componente de B e E) — cada um deles um emaranhado de coordenadas, multiplicações e subtrações.
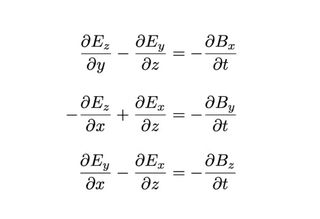
O poder da perseverança
Escolhi uma das equações de Maxwell como exemplo porque o peculiar escocês James Clerk Maxwell foi o primeiro grande físico a reconhecer o poder do simbolismo vetorial compacto. Infelizmente, Hamilton não viveu para ver o endosso de Maxwell. Mas ele nunca desistiu de acreditar na sua nova forma de representar quantidades físicas.
A perseverança de Hamilton diante da rejeição popular realmente me emocionou, quando eu estava pesquisando meu livro sobre vetores. Ele esperava que um dia — “não importa quando” — pudesse ser agradecido por sua descoberta, mas isso não era vaidade. Foi uma excitação com as possíveis aplicações que ele imaginou.

Ele ficaria maravilhado com o fato de os vetores serem tão amplamente usados hoje e de poderem representar informações digitais e físicas. Mas ele ficaria especialmente satisfeito com o fato de que, na programação de rotações, os quatérnios ainda são frequentemente a melhor escolha – como NASA e os programadores de computação gráfica sabem.
Em reconhecimento às conquistas de Hamilton, os fãs de matemática refazer sua famosa caminhada todo dia 16 de outubro para comemorar o Dia de Hamilton. Mas todos nós usamos os frutos tecnológicos desse graffiti despretensioso todos os dias.
Este artigo editado foi republicado em A conversa sob uma licença Creative Commons. Leia o artigo original.



